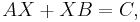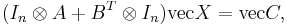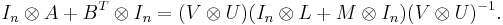Sylvester equation
The Sylvester equation, commonly encountered in control theory, is the matrix equation of the form
where 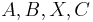 are
are 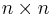 matrices.
matrices. 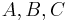 are known. The problem is to find
are known. The problem is to find  .
.
Contents |
Existence and uniqueness of the solution
Using the Kronecker product notation and the vectorization operator 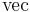 , we can rewrite the equation in the form
, we can rewrite the equation in the form
where 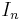 is the
is the 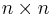 identity matrix. In this form, the Sylvester equation can be seen as a linear system of dimension
identity matrix. In this form, the Sylvester equation can be seen as a linear system of dimension 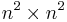 .[1]
.[1]
If 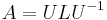 and
and 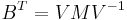 are the Jordan canonical forms of
are the Jordan canonical forms of  and
and 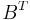 , and
, and 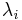 and
and 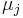 are their eigenvalues, one can write
are their eigenvalues, one can write
Since 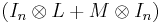 is upper triangular with diagonal elements
is upper triangular with diagonal elements 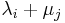 , the matrix on the left hand side is singular if and only if there exist
, the matrix on the left hand side is singular if and only if there exist  and
and  such that
such that 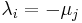 .
.
Therefore, we have proved that the Sylvester equation has a unique solution if and only if  and
and 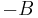 have no common eigenvalues.
have no common eigenvalues.
Numerical solutions
A classical algorithm for the numerical solution of the Sylvester equation is the Bartels–Stewart algorithm, which consists of transforming  and
and  into Schur form by a QR algorithm, and then solving the resulting triangular system via back-substitution. This algorithm, whose computational cost is O
into Schur form by a QR algorithm, and then solving the resulting triangular system via back-substitution. This algorithm, whose computational cost is O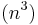 arithmetical operations, is used, among others, by LAPACK and the
arithmetical operations, is used, among others, by LAPACK and the lyap function in GNU Octave.
See also
References
1. J. Sylvester, Sur l’equations en matrices 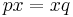 , C.R. Acad. Sci. Paris, 99 (1884), pp. 67 – 71, pp. 115 – 116.
, C.R. Acad. Sci. Paris, 99 (1884), pp. 67 – 71, pp. 115 – 116.
2. R. H. Bartels and G. W. Stewart, Solution of the matrix equation 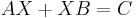 , Comm. ACM, 15 (1972), pp. 820 – 826.
, Comm. ACM, 15 (1972), pp. 820 – 826.
3. R. Bhatia and P. Rosenthal, How and why to solve the operator equation 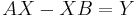 ?, Bull. London Math. Soc., 29 (1997), pp. 1 – 21.
?, Bull. London Math. Soc., 29 (1997), pp. 1 – 21.
4. S.-G. Lee and Q.-P. Vu, Simultaneous solutions of Sylvester equations and idempotent matrices separating the joint spectrum, Linear Algebra and its Applications, 435 (2011), pp. 2097 – 2109.
Notes
- ^ However, rewriting the equation in this form is not advised for the numerical solution since this version is costly to solve and can be ill-conditioned.